人口增长模型的改进与拓展

一、问题描述

在课堂上，我们对于美国人口预测，建立了马尔萨斯人口模型和阻滞增长模型。

结合课堂上所给的建模思路和数据，思考如下问题：

针对所给数据情况，还能有什么方法可解决问题，并说明所给方法与现有方法的优略
针对现有问题，还有什么可拓展研究的思路？并给出具体模型

二、模型改进

原有模型

关于人口预测模型，我们假设了人口数量增长的一般规律，即

\[下一时刻人口数 = 当前人口数 + 一定时间内人口增量\]

其中，

\[一定时间内人口增量 = 当前人口数 × 人口增长率\]

因为环境资源有限，随着人口总数的增加，人口增长率会逐渐减少，最终减少为0，此时达到人口最大限度。

以上各变量可分别用符号表示为

符号	含义
\(P(t)\)	\(t\)时刻人口数
\(P(t+\Delta t)\)	\(t\)时刻的下一时刻人口数
\(r\)	若无环境制约时的人口增长率，为常数
\(r(P)\)	人口增长率
\(\kappa\)	总人口上限
\(P_0\)	最初人口数

则有

\[P(t+\Delta t)=P(t)+r(P) P(t) \Delta t\] \[r(P)=r(1-\frac{P}{\kappa})\]

假设人口增长是连续的，当\(\Delta t\)趋于0时，则有

\[\frac{dP}{dt}=r(1-\frac{P}{\kappa})P\]

进而求解微分方程，得出结果。

改进模型

在上述问题中，我们假设了环境资源不变，人口上限为一定值。但是在实际生活中，随着社会的发展，人口的增加，生产力也在不断提升，人类可利用资源也在不断增加，因此，环境资源是与人口数有关的。鉴于此，上述模型中的总人口上限应更大一些。

假设在基础环境承载力基础上，每\(N\)个人可以为一个人创造额外的生存资料，所以环境承载力可以表示为\(\kappa+\frac{P}{N}\)

则人口增长速率可表示为： \(\frac{dP}{dt}=r(1-\frac{P}{\kappa+\frac{P}{N}})P\)

然而我们发现当\(N\)作为变量出现时，解析解较为复杂，且不易计算

不妨取\(N=2\)，即每两个人可以为一个人提供生存资料，这符合人类一对夫妻为一个孩子提供生存资料的现实背景。

我们得到微分方程

\[\begin{cases} \frac{dP}{dt}=r(1-\frac{P}{\kappa+\frac{P}{2}})P \\ P(0)=P_0 \end{cases}\]

求解，得

\[P(t)=2[\kappa+\frac{\kappa-\frac{P_0}{2}}{P_0 e^{r t}}(\kappa-\frac{P_0}{2}-\sqrt{2\kappa P_0 e^{r t}+(\kappa-\frac{P_0}{2})^2})]\]

模型应用

我们以美国人口数据来检测该模型的合理性，编写以下程序：

import numpy as np 
import pandas as pd
from matplotlib import pyplot as plt 
from scipy.optimize import curve_fit

data = pd.DataFrame(pd.read_csv('data.csv'),dtype=float)

data_size = len(data)
year = np.arange(data_size)

def loss(pred,real):
    return np.abs(pred-real)/real

def percentage(x):
    return "%.2f%%" % (x * 100)

def fit_display(f):
    popt, _ = curve_fit(f,year,data.population/1000)
    print('parameters:',popt)
    pred = f(year,*popt)*1000

    result = data.copy()
    result['prediction'] = np.round(pred,2)
    loss_ = loss(pred,data.population)
    result['loss'] = np.asarray(list(map(percentage,loss_)))
    print('loss:',percentage(np.mean(loss_)))

    plt.scatter(data.year,data.population,label='real data')
    plt.plot(data.year,pred,'r-',label = 'prediction')
    plt.legend()

    return result

def f(t,r,k):
    j = k - P0/2
    e = P0*np.exp(r*t)
    return 2*(k+j*(j-np.sqrt(2*k*e+j**2))/e)

fit_display(f)

'''
Copyright 2020 by Algebra-FUN
ALL RIGHTS RESERVED.
'''

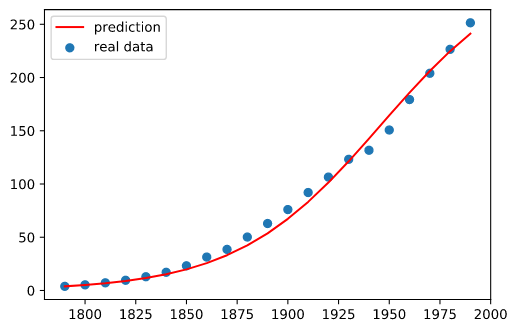
我们得到实际人口与预测人口的比较如下图和表：

year	population	prediction	loss
1790	3.9	3.90	0%
1800	5.3	5.14	3.05%
1810	7.2	6.76	6.09%
1820	9.6	8.88	7.47%
1830	12.9	11.64	9.74%
1840	17.1	15.22	10.99%
1850	23.2	19.82	14.56%
1860	31.4	25.70	18.17%
1870	38.6	33.11	14.22%
1880	50.2	42.35	15.63%
1890	62.9	53.67	14.67%
1900	76.0	67.27	11.49%
1910	92.0	83.19	9.57%
1920	106.5	101.33	4.85%
1930	123.2	121.33	1.52%
1940	131.7	142.59	8.27%
1950	150.7	164.37	9.07%
1960	179.3	185.83	3.64%
1970	204.0	206.18	1.07%
1980	226.5	224.78	0.76%
1990	251.4	241.24	4.04%

我们将我们的代码和实验结果上传至 GitHub

如果您想查看更多详情，欢迎访问：https://github.com/Algebra-FUN/My-Math-Model/tree/master/1

可以观察到，预测函数具有较高的精确度。由此可见，我们的模型是合理而有意义的。

模型评价

该模型在原有模型的基础上，考虑了随着人口数的变化，环境资源也会增加这一问题，提高了模型的科学性与合理性。而且从结果上看，该模型对美国人口预测具有很高的应用价值。

三、拓展研究

提出问题

在上文问题的求解中，我们对于增长速率r的选取是进行充分理想化的，实际上r的数值与人口结构密切相关。Malthus和LOGISTIC模型基于宏观人口数据进行研究，因此未能揭示人口结构对人口发展的影响。因此，我们希望能得到一种模型，了解人口结构对人口发展的作用。

研究思路

我们知道LESLIE模型是一种“可以利用某一初始时刻种群的年龄分布，动态地预测种群年龄分布及数量随时间的演变过程”的模型，然而LESLIE模型一般用于生物种群数量预测，而人类的繁殖要比生物生殖复杂许多，所以我们需要将原始LESLIE模型的Malthus增长函数替换为LOGISTIC增长函数，以适应现代国家人类人口的变化规律。

模型建立

模型假设

研究的种群处于一个相对安定的社会，无突发性事件影响
各年龄段的生育率和存活率只受人口数量因素间接影响，与时间无关，排除政治、生态等因素的影响
各年龄段的生育率由于人口增加，造成生存压力增加，而会导致生育率下降，符合LOGISTIC增长率函数
各年龄段的存活率相对稳定，故假定为恒定
由于100岁以上老人比例很低，故排除100岁以上老人对整体人口的影响，并设定年龄上限为100岁
由于数据精度和计算量的原因，故将每10岁划分为一个年龄段

符号	含义
\(t\)	从开始的第\(t\)年，\(t\in \mathbb{N}\)
\(x\)	第\(x\)个年龄段,即\(年龄\in[10(x-1),10x),x\in\{1,2,\dots,10\}\)
\(P_x(t)\)	第\(t\)年第\(x\)个年龄段的人口数量
\(P(t)\)	第\(t\)年总人口数
\(\vec{P}(t)\)	第\(t\)年人口向量，\(\vec{P}(t)=(P_1(t),P_2(t),\dots,P_{10}(t))\)
\(F_x(P)\)	第\(x\)个年龄段生育率关于总人口的函数
\(S_x\)	第\(x\)个年龄段存活率，为恒定常数
\(\kappa\)	总人口数上限

模型求解

LESLIE矩阵

\[L(P)= \left[ \begin{matrix} F_1(P) & F_2(P) & \cdots & F_9(P) &F_{10}(P) \\ S_1 \\ & S_2 \\ && \ddots \\ &&& S_9 \end{matrix} \right]\]

第\(t+1\)年人口向量可由第\(t\)年人口向量得出

\[\vec{P}(t+1)=L(P)\vec{P}(t)\]

即， \(\left[ \begin{matrix} P_1(t+1)\\ P_2(t+1)\\ \vdots\\ P_9(t+1)\\ P_{10}(t+1) \end{matrix} \right] = \left[ \begin{matrix} F_1(P) & F_2(P) & \cdots & F_9(P) &F_{10}(P) \\ S_1 \\ & S_2 \\ && \ddots \\ &&& S_9 \end{matrix} \right] \left[ \begin{matrix} P_1(t)\\ P_2(t)\\ \vdots\\ P_9(t)\\ P_{10}(t) \end{matrix} \right]\)

经过查阅大量资料，中国国家统计局公布数据仅有历次人口普查的数据中有详细年龄段数据，由于历次普查相隔时间较大，因而数据缺乏导致编程数值计算能力不足，故不实际求解

人口增长模型拓展

数模课作业1